At math conferences all over the world, of late, mathematicians have been seen lingering in darkened lecture halls, peering at multi-media screens and sporting one-eye-red/one-eye-blue, 3-D glasses. Before them stands mathematician Jeff Weeks, presenting his model of the universe: a twelve-sided figure known as a dodecahedron. To the untrained eye, it is a magnified mass of honeycomb, with each side of each cell flashing in multicolour as it rotates through a background of endless black.
We humans have been trying to figure out the shape of the universe since Antiquity. In ancient Greece, using bare-hands science and the power of their imaginations, philosophers Leucippus and Democritus envisaged an infinite universe. Aristotle fathomed it as a finite ball, with the Earth at the centre. Aristotle’s view prevailed and went mostly unchallenged in Western society for almost 2,000 years, until the invention of the telescope by Galileo in 1608. In 1917, when Einstein applied his geometrical explanation of gravity (his famous theory of relativity) to the questions of cosmology, he recycled a three-sphere scenario previously posited by Bernhard Riemann. All hypotheses, dating from ancient times to today, remain contentious. Technological advances over the last decade, however, have increased our chances of actually finding an answer to this age-old question.
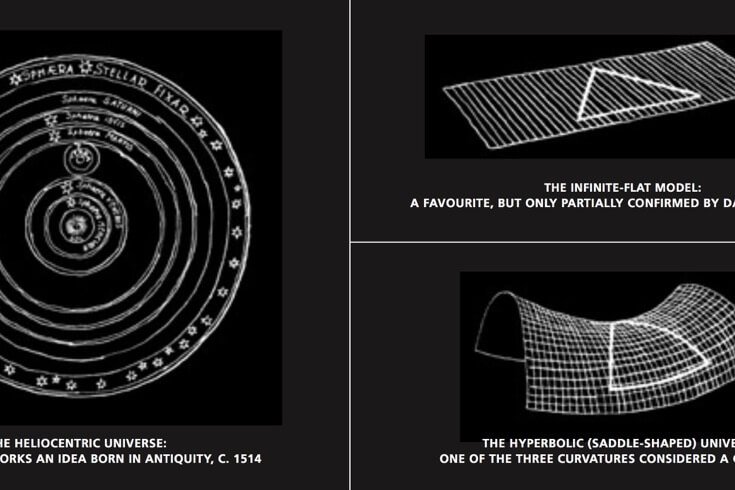
Currently, there are three classes of shapes considered to be contenders, each based on a posited curvature of the universe: the spherical, the hyperbolic (saddle-shaped), and, the favourite of the moment, the “standard model,” which predicts an infinite and flat universe, forever expanding under the pressure of an (as yet) inexplicable “dark energy.” Now, Weeks and a team of Parisian cosmologists have found a new plausible model: the dodecahedron.
Weeks, based in Canton, New York, is a geometer – by the classical definition, one who measures space, as in geometry. He is the beneficiary of a 1999 MacArthur fellowship, the so-called “genius award,” which generously funds recipients to pursue their interests with no strings attached. Weeks, who is forty-seven, has been wondering about the shape of the universe since he was a teenager, but always theoretically – using mental images and sketches initially, and later numbers and equations as his tools. “The attraction was very much an aesthetic one,” he says. “The different possible shapes for the universe are so beautiful – the appeal of geometry is describing real space, and the universe is the ultimate space.”
Five years ago, out of the blue, Weeks got an email from a cosmologist asking a technical question about the vibrational modes of a particular spatial manifold. Weeks did not have an answer to the query, but he offered to find one and asked, by the way, why the interest? When he discovered cosmologists were expecting hard data from outer space that would allow them to test the shape of the real universe, his already wide eyes widened some more. “This was a dream come true for a theoretical mathematician,” he says, “to finally have some data on the way.” Before he knew it, he was collaborating with the cosmologists.
Weeks’s task, through a continuous process of back-and-forth with his cohorts, was to provide the raw materials. First he determined which geometrical structures were plausible shapes for the universe by playing around within existing classes. Second, he calculated how each would behave in space. Both tasks involved a lot of sitting around and pondering, pencil and paper in hand, fiddling with the mathematics. Then he had to work up formulas to prove his hypotheses. Finally, he devised computer programs to run his formulas. After that, it was over to the cosmologists – Jean-Pierre Luminet, Alain Riazuelo, Roland Lehoucq, and Jean-Philippe Uzan. They plugged Weeks’s geometric formulas into simulations based on assumptions about the physics of the universe. The results would be compared to reality – that is, the data soon to arrive from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP).
The WMAP probe was sent up to map cosmic microwave background radiation, the echo of the origin of the universe – the assumed big bang – and provide data about its early history and scale. One particularly useful indicator of universe topology is the temperature fluctuations of radiation emanating from the big bang. In a recent article in Nature magazine, Weeks and the cosmologists explained these fluctuations by comparing them with the sound waves of musical harmonics:
“A musical note is the sum of a fundamental, a second harmonic, a third harmonic, and so on. The relative strengths of the harmonics – the note’s spectrum – determines the tone quality, distinguishing, say, a sustained middle C played on a flute from the same note played on a clarinet. Analogously, the temperature map on the microwave sky is the sum of spherical harmonics. The relative strength of the harmonics – the power spectrum – is a signature of the physics and geometry of the universe.”
When the WMAP data arrived in February, 2003, it confirmed the prevailing infinite-flat model, but only partially. All the small and medium-sized temperature waves were present as predicted. But the model failed when it came to finding the broad wavelengths that should exist in such a large and infinite universe. The probe found none. One explanation, says Weeks, is that space simply isn’t that big and thus could never produce such large waves in the first place. “A violin is never going to play the low notes of a cello because a violin’s strings aren’t long enough to support such a long sound wave,” he says. “It’s the same with the universe. Its waves cannot be larger than space itself.”
Enter the finite-dodecahedron model. The behaviour Weeks predicted for a dodecahedral universe matched all the WMAP data. “It was a very pleasant surprise,” he says. “Our model fit even better than we expected.” The future of dodecahedral space, however, still faces two major challenges. First, the model’s calculations of spatial curvature must be compared to forthcoming, more precise data from the Planck Probe (launching in 2007). The results of the probe will either fine-tune Weeks’s model or refute it entirely. Second, it must pass the “circles-in-the-sky” test. If the model is correct, a computer-coded search should be able to detect six pairs of matching circles across the cosmic horizon – echoes from the big bang vibrating against the twelve faces of the dodecahedron universe.
“So far, we have found no matching circles,” says Glenn Starkman, one of the circle searchers. Starkman, who broke ground on his universe-topology work at the Canadian Institute for Theoretical Astrophysics, is spending his sabbatical from Case Western in Cleveland at the European Organisation for Nuclear Research (CERN) in Geneva. He and his team are running new tests of the computer coding to be doubly sure the circles would have been found if they were there – it’s possible that galactic contamination obscured their results. He estimates they will have a definitive answer soon.
Weeks and his team, meanwhile, are at once sticking to their proposition and exploring other options, such as the possibility of a universe that is finite in some directions and infinite in others. “You don’t want to ignore the other possibilities,” says Weeks. “But personally, I’m not quite ready to declare the circles missing.”
The dodecahedron universe, if it holds up, has implications for quantum mechanics and theories of the big bang and, even more promisingly, for a deeper and more beautiful understanding of the blinking night sky and the potential of travelling into its depths. “Hypothetically,” says Weeks, “if you head off into a dodecahedral universe you would travel in a straight line and come back to the starting point. But it would take a long, long time.”
The model also leaves us with a new question: If the universe is finite, what is beyond? “Nothing,” says Weeks, “but it is a very profound nothing. The best answer to that question is to make the question go away.” And with a bit of elaborate reasoning, he can.